Project 4: Machine Learning

Due: Wednesday, December 11, 5pm EDT.

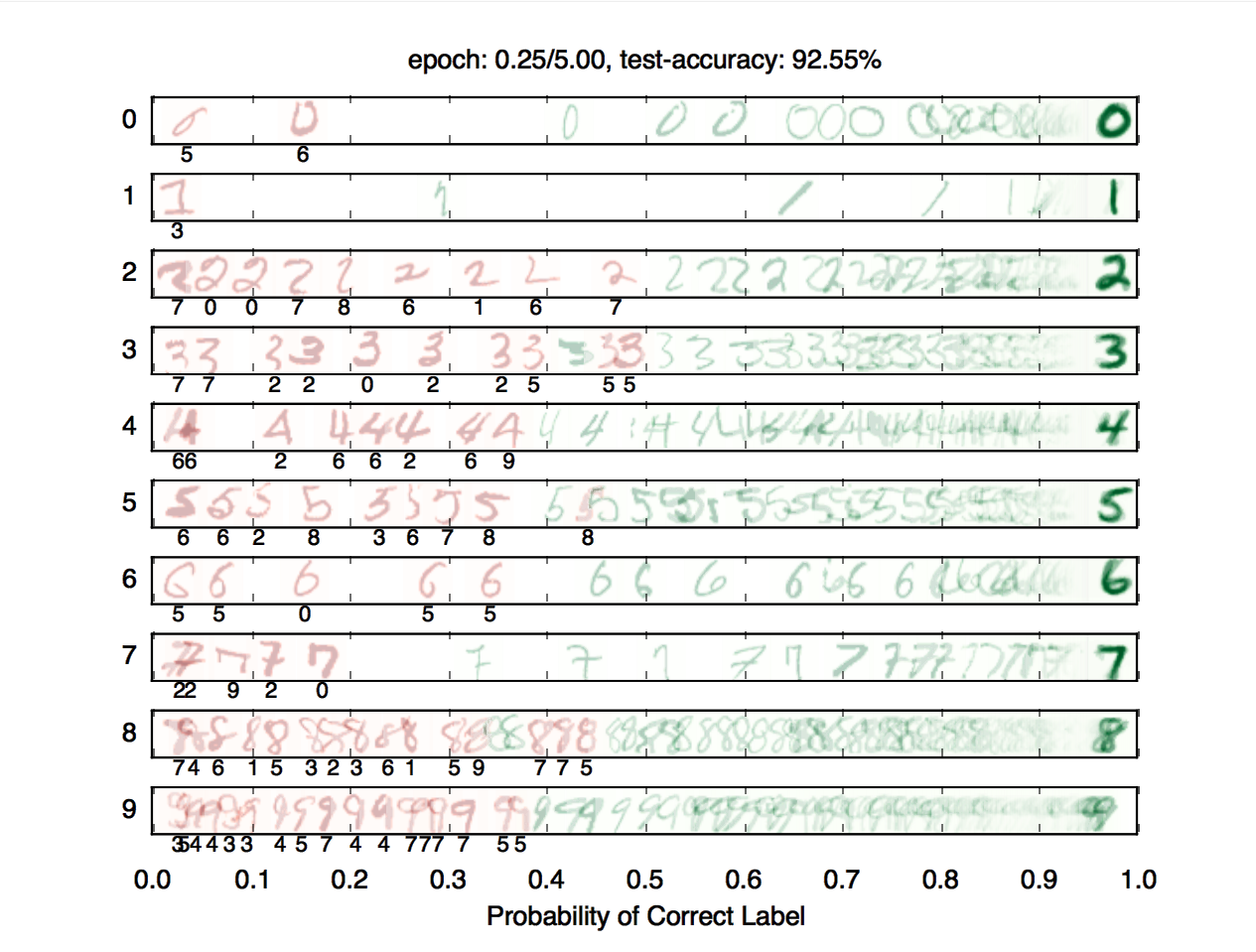
Digit classification

Introduction
Installation
Project Provided Code (Part I)
Question 1 (6 points): Perceptron
Neural Network Tips
Example: Linear Regression
Question 2 (6 points): Non-linear Regression
Question 3 (6 points): Digit Classification
Submission

Introduction

This project will be an introduction to machine learning; you will build a neural network to classify digits, and more!

The code for this project contains the following files, available as a zip archive.

Files you'll edit:
`models.py`	Perceptron and neural network models for a variety of applications.
Supporting files you can ignore:
`autograder.py`	Project autograder.
`backend.py`	Backend code for various machine learning tasks.
`data`	Datasets for digit classification.

Files to Edit and Submit: You will fill in portions of models.py during the assignment. Please do not change the other files in this distribution.

Evaluation: Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation – not the autograder’s judgements – will be the final judge of your score. If necessary, we will review and grade assignments individually to ensure that you receive due credit for your work.

Academic Dishonesty: We will be checking your code against other submissions in the class for logical redundancy. If you copy someone else’s code and submit it with minor changes, we will know. These cheat detectors are quite hard to fool, so please don’t try. We trust you all to submit your own work only; please don’t let us down. If you do, we will pursue the strongest consequences available to us.

Getting Help: You are not alone! If you find yourself stuck on something, contact the course staff for help. Office hours, section, and the discussion forum are there for your support; please use them. If you can’t make our office hours, let us know and we will schedule more. We want these projects to be rewarding and instructional, not frustrating and demoralizing. But, we don’t know when or how to help unless you ask.

Discussion: Please be careful not to post spoilers.

Installation

If the following runs and you see the below window pop up where a line segment spins in a circle, you can skip this section. You should use the conda environment for this since conda comes with the libraries we need.

python autograder.py --check-dependencies

Plot of a line

For this project, you will need to install the following two libraries:

numpy, which provides support for fast, large multi-dimensional arrays.
matplotlib, a 2D plotting library.
Pytorch, a neural network library.

We recommend using a conda environment if you have one. If you have a conda environment, you can install the first two packages on the command line by running:

conda activate [your environment name]

pip install numpy
pip install matplotlib

You will not be using these two libraries directly, but they are required in order to run the provided code and autograder.

If your setup is different, you can refer to numpy and matplotlib installation instructions. You can use either pip or conda to install the packages; pip works both inside and outside of conda environments.

You can then follow the instructions here: Pytorch to download the latest version of Pytorch using either Conda or Pip. If you haven’t used Pytorch before, please use the CPU version. The CPU version of Pytorch is the least likely to cause any bugs or complications.

After installing, try the dependency check.

Project Provided Code (Part I)

Here are a the main functions you should be using. This list is not exhaustive, we have imported all the functions you may use in models.py and encourage you to look at the pytorch documentation for additional guidelines on how you should use them.

tensor(): Tensors are the primary data structure in pytorch. They work very similarly to Numpy arrays in that you can add and multiply them. Anytime you use a pytorch function or feed an input into a neural network, you should try to make sure that your input is in the form of a tensor. You can change a python list to a tensor as such: tensor(data) where data is your n-dimentional list.
relu(input): The pytorch relu activation is called as such: relu(input). It takes in an input, and returns max(input, 0).
Linear: Use this class to implement a linear layer. A linear layer takes the dot product of a vector containing your weights, and the input. You must initialize this in your __init__ function like so: self.layer = Linear(length of input vector, length of output vector) and call it as such when running your model: self.layer(input). When you define a linear layer like this, Pytorch automatically creates weights and updates them during training.
movedim(input_vector, initial_dimension_position, final_dimension_position): This function takes in a matrix, and swaps the initial_dimension_position(passed in as an int), with final_simension_position. This will be helpful in question 3.
cross_entropy(prediction, target): This function should be your loss function for any classification tasks(Question 3). The further away your prediction is from the target, the higher a value this will return.
mse_loss(prediction, target): This function should be your loss function for any regression tasks(Question 2). It can be used in the same way as cross_entropy.

All the data in the project will be provided to you in the form of a pytorch dataset object, which you will be transforming into a pytorch dataloader in order to help you easily create batch sizes.

>>> data = DataLoader(training_dataset, batch_size = 64)
>>> for batch in data:
>>>   #Training code goes here

For all of these questions, every batch returned by the DataLoader will be a dictionary in the form: {‘x’:features, ‘label’:label} with label being the value(s) we want to predict based off of the features.

Question 1 (6 points): Perceptron

Before starting this part, be sure you have numpy and matplotlib installed!

In this part, you will implement a binary perceptron. Your task will be to complete the implementation of the PerceptronModel class in models.py.

For the perceptron, the output labels will be either 1 or −1, meaning that data points (x, y) from the dataset will have y be a torch.Tensor that contains either 1 or −1 as its entries.

Your tasks are to:

Fill out the init(self, dimensions) function. This should initialize the weight parameter in PerceptronModel. Note that here, you should make sure that your weight variable is saved as a Parameter() object of dimension 1 by dimensions. This is so that our autograder, as well as pytorch, recognize your weight as a parameter of your model.
Implement the run(self, x) method. This should compute the dot product of the stored weight vector and the given input, returning an Tensor object.
Implement get_prediction(self, x), which should return 1 if the dot product is non-negative or −1 otherwise.
Write the train(self) method. This should repeatedly loop over the data set and make updates on examples that are misclassified. When an entire pass over the data set is completed without making any mistakes, 100% training accuracy has been achieved, and training can terminate.
Luckily, Pytorch makes it easy to run operations on tensors. If you would like to update your weight by some tensor direction and a constant magnitude, you can do it as follows: self.w += direction * magnitude

For this question, as well as all of the remaining ones, every batch returned by the DataLoader will be a dictionary in the form: {‘x’:features, ‘label’:label} with label being the value(s) we want to predict based off of the features.

To test your implementation, run the autograder:

python autograder.py -q q1

Note: the autograder should take at most 20 seconds or so to run for a correct implementation. If the autograder is taking forever to run, your code probably has a bug.

Neural Network Tips

In the remaining parts of the project, you will implement the following models:

Q2: Non-linear Regression
Q3: Handwritten Digit Classification

Building Neural Nets

Throughout the applications portion of the project, you’ll use Pytorch to create neural networks to solve a variety of machine learning problems. A simple neural network has linear layers, where each linear layer performs a linear operation (just like perceptron). Linear layers are separated by a non-linearity, which allows the network to approximate general functions. We’ll use the ReLU operation for our non-linearity, defined as $\text{relu}(x)=\max(x,0)$ . For example, a simple one hidden layer/ two linear layers neural network for mapping an input row vector $\mathbf x$ to an output vector $\mathbf f(\mathbf x)$ would be given by the function:

\mathbf f(\mathbf x)=\text{relu}(\mathbf x \cdot \mathbf{W_1}+\mathbf{b_1}) \cdot \mathbf{W_2} + \mathbf{b_2}

where we have parameter matrices $\mathbf{W_1}$ and $\mathbf{W_2}$ and parameter vectors $\mathbf{b_1}$ and $\mathbf{b_2}$ to learn during gradient descent. $\mathbf{W_1}$ will be an $i \times h$ matrix, where $i$ is the dimension of our input vectors $\mathbf{x}$ , and $h$ is the hidden layer size. $\mathbf{b_1}$ will be a size $h$ vector. We are free to choose any value we want for the hidden size (we will just need to make sure the dimensions of the other matrices and vectors agree so that we can perform the operations). Using a larger hidden size will usually make the network more powerful (able to fit more training data), but can make the network harder to train (since it adds more parameters to all the matrices and vectors we need to learn), or can lead to overfitting on the training data.

We can also create deeper networks by adding more layers, for example a three-linear-layer net:

\mathbf{\hat y} = \mathbf{f}(\mathbf{x}) = \mathbf{\text{relu}(\mathbf{\text{relu}(\mathbf{x} \cdot \mathbf{W_1} + \mathbf{b_1})} \cdot \mathbf{W_2} + \mathbf{b_2})} \cdot \mathbf{W_3} + \mathbf{b_3}

Or, we can decompose the above and explicitly note the 2 hidden layers:

\mathbf{h_1} = \mathbf{f_1}(\mathbf{x}) = \text{relu}(\mathbf{x} \cdot \mathbf{W_1} + \mathbf{b_1})

\mathbf{h_2} = \mathbf{f_2}(\mathbf{h_1}) = \text{relu}(\mathbf{h_1} \cdot \mathbf{W_2} + \mathbf{b_2})

\mathbf{\hat y} = \mathbf{f_3}(\mathbf{h_2}) = \mathbf{h_2} \cdot \mathbf{W_3} + \mathbf{b_3}

Note that we don’t have a $\text{relu}$ at the end because we want to be able to output negative numbers, and because the point of having $\text{relu}$ in the first place is to have non-linear transformations, and having the output be an affine linear transformation of some non-linear intermediate can be very sensible.

Batching

For efficiency, you will be required to process whole batches of data at once rather than a single example at a time. This means that instead of a single input row vector $\mathbf{x}$ with size $i$ , you will be presented with a batch of $b$ inputs represented as a $b \times i$ matrix $\mathbf{X}$ . We provide an example for linear regression to demonstrate how a linear layer can be implemented in the batched setting.

Randomness

The parameters of your neural network will be randomly initialized, and data in some tasks will be presented in shuffled order. Due to this randomness, it’s possible that you will still occasionally fail some tasks even with a strong architecture – this is the problem of local optima! This should happen very rarely, though – if when testing your code you fail the autograder twice in a row for a question, you should explore other architectures.

Designing Architecture

Designing neural nets can take some trial and error. Here are some tips to help you along the way:

Be systematic. Keep a log of every architecture you’ve tried, what the hyperparameters (layer sizes, learning rate, etc.) were, and what the resulting performance was. As you try more things, you can start seeing patterns about which parameters matter. If you find a bug in your code, be sure to cross out past results that are invalid due to the bug.
Start with a shallow network (just one hidden layer, i.e. one non-linearity). Deeper networks have exponentially more hyperparameter combinations, and getting even a single one wrong can ruin your performance. Use the small network to find a good learning rate and layer size; afterwards you can consider adding more layers of similar size.
If your learning rate is wrong, none of your other hyperparameter choices matter. You can take a state-of-the-art model from a research paper, and change the learning rate such that it performs no better than random. A learning rate too low will result in the model learning too slowly, and a learning rate too high may cause loss to diverge to infinity. Begin by trying different learning rates while looking at how the loss decreases over time.
Smaller batches require lower learning rates. When experimenting with different batch sizes, be aware that the best learning rate may be different depending on the batch size.
Refrain from making the network too wide (hidden layer sizes too large) If you keep making the network wider accuracy will gradually decline, and computation time will increase quadratically in the layer size – you’re likely to give up due to excessive slowness long before the accuracy falls too much. The full autograder for all parts of the project takes ~12 minutes to run with staff solutions; if your code is taking much longer you should check it for efficiency.
If your model is returning Infinity or NaN, your learning rate is probably too high for your current architecture.
Recommended values for your hyperparameters:
- Hidden layer sizes: between 100 and 500.
- Batch size: between 1 and 128. For Q2 and Q3, we require that total size of the dataset be evenly divisible by the batch size.
- Learning rate: between 0.0001 and 0.01.
- Number of hidden layers: between 1 and 3(It’s especially important that you start small here).

Example: Linear Regression

As an example of how the neural network framework works, let’s fit a line to a set of data points. We’ll start four points of training data constructed using the function $y=7x_0+8x_1+3$ . In batched form, our data is:

\mathbf X=\begin{bmatrix} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{bmatrix} \qquad \mathbf Y = \begin{bmatrix} 3 \\ 11 \\ 10 \\ 18 \end{bmatrix}

Suppose the data is provided to us in the form of Tensors.

>>> x
torch.Tensor([[0,0],[0,1],[1,0],[1,1])
>>> y
torch.Tensor([[3],[11],[10],[18]])

Let’s construct and train a model of the form $f(\mathbf x)=x_0\cdot m_0+x_1 \cdot m_1+b$ . If done correctly, we should be able to learn that $m_0=7$ , $m_1=8$ , and $b=3$ .

First, we create our trainable parameters. In matrix form, these are:

\mathbf M = \begin{bmatrix} m_0 \\ m_1 \end{bmatrix} \qquad \mathbf B = \begin{bmatrix} b \end{bmatrix}

Which corresponds to the following code:

m = Tensor(2, 1)
b = Tensor(1, 1)

A minor detail to remember is that tensors get initialized with all 0 values unless you initialize the tensor with data. Thus, printing them gives:

>>> m
torch.Tensor([[0],[0]])
>>> b
torch.Tensor([[0]])

Next, we compute our model’s predictions for y. If you’re working on the pytorch version, you must define a linear layer in your __init__() function as mentioned in the definition that is provided for Linear above.:

predicted_y = self.Linear_Layer(x)

Our goal is to have the predicted $y$ -values match the provided data. In linear regression we do this by minimizing the square loss:

\mathcal{L} = \frac{1}{2N}\sum_{(\mathbf x,y)}(y-f(\mathbf x))^2

We calculate our loss value:

loss = mse_loss(predicted_y, y)

Finally, after defining your neural network, In order to train your network, you will first need to initialize an optimizer. Pytorch has several built into it, but for this project use: optim.Adam(self.parameters(), lr=lr) where lr is your learning rate. Once you’ve defined your optimizer, you must do the following every iteration in order to update your weights:

Reset the gradients calculated by pytorch with optimizer.zero_grad()
Calculate your loss tensor by calling your get_loss() function
Calculate your gradients using loss.backward(), where loss is your loss tensor returned by get_loss
And finally, update your weights by calling optimizer.step()

You can look at the official pytorch documentation for an example of how to use a pytorch optimizer().

Question 2 (6 points): Non-linear Regression

For this question, you will train a neural network to approximate $\sin(x)$ over $[-2\pi, 2\pi]$ .

You will need to complete the implementation of the RegressionModel class in models.py. For this problem, a relatively simple architecture should suffice (see Neural Network Tips for architecture tips). Use mse_loss from Pytorch as your loss.

Your tasks are to:

Implement RegressionModel.__init__ with any needed initialization.
Implement RegressionModel.run(RegressionModel.forward in pytorch) to return a batch_size by 1 node that represents your model’s prediction.
Implement RegressionModel.get_loss to return a loss for given inputs and target outputs.
Implement RegressionModel.train, which should train your model using gradient-based updates.

There is only a single dataset split for this task (i.e., there is only training data and no validation data or test set). Your implementation will receive full points if it gets a loss of 0.02 or better, averaged across all examples in the dataset. You may use the training loss to determine when to stop training. Note that it should take the model a few minutes to train.

python autograder.py -q q2

Question 3 (6 points): Digit Classification

For this question, you will train a network to classify handwritten digits from the MNIST dataset.

Each digit is of size 28 by 28 pixels, the values of which are stored in a 784-dimensional vector of floating point numbers. Each output we provide is a 10-dimensional vector which has zeros in all positions, except for a one in the position corresponding to the correct class of the digit.

Complete the implementation of the DigitClassificationModel class in models.py. The return value from DigitClassificationModel.run() should be a batch_size by 10 node containing scores, where higher scores indicate a higher probability of a digit belonging to a particular class (0-9). You should use cross_entropy from Pytorch as your loss. Do not put a ReLU activation in the last linear layer of the network.

In addition to training data, there is also validation data and a test set. You can use dataset.get_validation_accuracy() to compute validation accuracy for your model, which can be useful when deciding whether to stop training. The test set will be used by the autograder.

To receive points for this question, your model should achieve an accuracy of at least 97% on the test set. For reference, our staff implementation consistently achieves an accuracy of 98% on the validation data after training for around 5 epochs. Note that the test grades you on test accuracy, while you only have access to validation accuracy – so if your validation accuracy meets the 97% threshold, you may still fail the test if your test accuracy does not meet the threshold. Therefore, it may help to set a slightly higher stopping threshold on validation accuracy, such as 97.5% or 98%.